Anomaly Detection - Outliers

1. Regression with Python

2. Simple Linear Regression

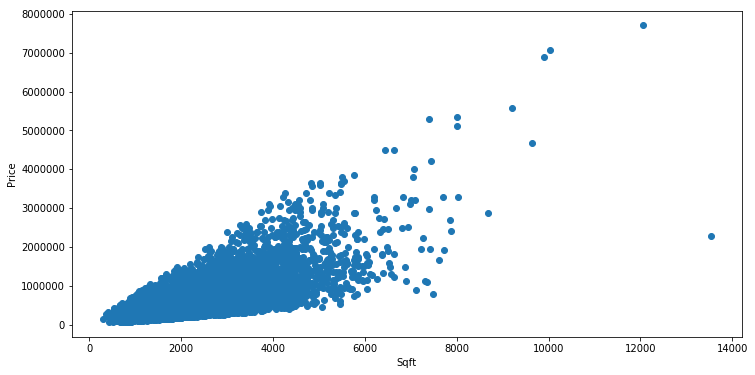
3. Multiple Regression

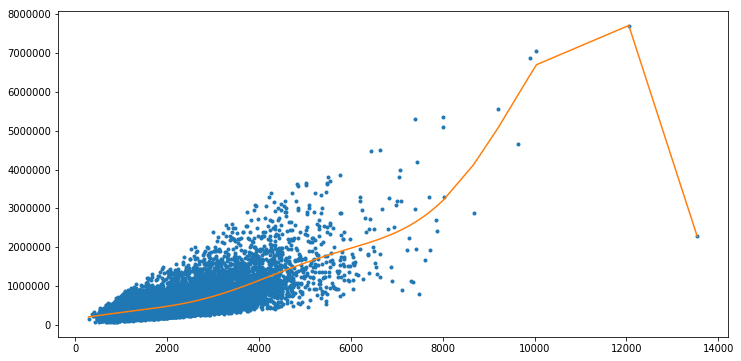
4. Local Regression

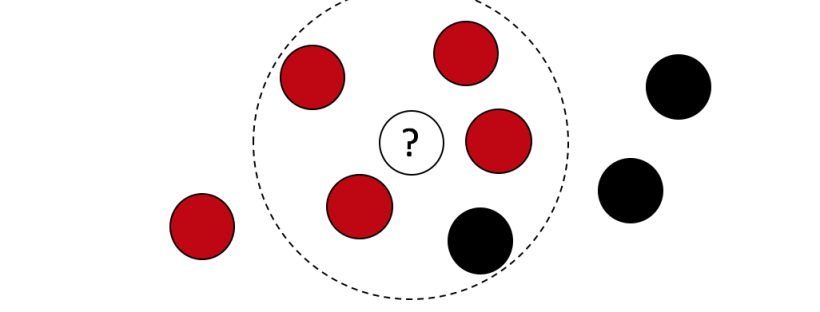
5. Anomaly Detection - K means

6. Anomaly Detection - Outliers

Point anomalies on test responding

It is mainly important to analyze all the features involved in every test taken by a person, and it is straightforward thinking that not all tasks are with full concentration because the nature of the tool, is an app, and we might expect the people taking the test can get distracted by some random reason

The main objective here is to analyze any pattern related to the time in milliseconds a participant spend on responding every visual task.

png

In [None]:

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

In [None]:

color_ms = '#386cb0' #blue, This is the color chosen for patients with Multiple Sclerosis
color_hc = 'red'#This is the color chosen for health control participants

In [None]:

df_measures_users = pd.read_csv('https://s3.eu-west-3.amazonaws.com/pedrohserrano-datasets/df_measures_users.csv', encoding="utf-8")

In [None]:

df_symbols = pd.read_csv('https://s3.eu-west-3.amazonaws.com/pedrohserrano-datasets/df_symbols.csv', encoding="utf-8")

In [None]:

score_variable = 'correct.answers'

Population of Study

In [None]:

print('{} Data points distribuited among {} Participants'.format(len(df_symbols), len(df_measures_users)))

We choose the score variable as the number of correct answers on every test

In [None]:

#Split the patients MS (Multiple Sclerosis) and HC (Health Control)
df_ms = df_measures_users[df_measures_users['ms']==1]
df_hc = df_measures_users[df_measures_users['ms']==0]

In [None]:

print('Patients on MS group: {} ({}%)\nPatients on HC group: {} ({}%) '.format(
        len(df_ms), round(len(df_ms)/len(df_measures_users)*100, 0),
        len(df_hc), round(len(df_hc)/len(df_measures_users)*100, 0)))

In [None]:

plt.figure(figsize=[16, 8])
sns.kdeplot(df_symbols[df_symbols['ms']==1][score_variable], color='red', label='MS')
sns.kdeplot(df_symbols[df_symbols['ms']==0][score_variable], color='blue', label='HC')
plt.title('Scores Distribution MS and HC Groups')

Defining Boundary

The first thing we have to consider is the time.

So we define $ \Delta_{tr} $ as the time elapsed between 2 trials, where a trial is the event of push the buttom and select a digit on the test.

Thinking on this we say that every person perform $n$ number of tests and every test has $m$ number of trials, then the time elapsed to perform every trial is $ \Delta_{tr} $

We define $T$ as the vector of time responses on an event, following this logic we can calculate the median of those times.

Finally we may calculate the $SD$ of all the people on MS and Health Control grou separatelly

Distraction Points

$\Delta_{tr} > median(T) + 2 (SD (Group)) \hspace{1cm}$ $\max{\{\Delta_{tr},0\}} < median(T) - 2 (SD (Group)) \hspace{1cm} \forall{\Delta_{tr}}$

$T =(\Delta_{tr1}, \Delta_{tr2}, … \Delta_{trm})$ $tr =$ Time of response on a trial

In [None]:

print('Standart Deviation of every delta per group \n MS: {} \n HC: {}'.format(
df_symbols['response_ms_sd'].unique()[0], df_symbols['response_ms_sd'].unique()[1]))

Detecting Outliers

We can just take one single event on a random choise person (eobt3CosDzEtxWW5P) for instance, and plot the time of response in milisecond alongside the 90 seconds showing the symbols choosen on each task

In [None]:

df_user = df_symbols[df_symbols['userId']=='eobt3CosDzEtxWW5P']
stamps = df_user['timestamp'].unique()

plt.figure(figsize=(16, 4))
df_user_ts = df_user[df_user['timestamp']==stamps[0]]
plt.scatter(df_user_ts['trial'], df_user_ts['response_ms'], color=color_ms)
plt.hlines(y=df_user_ts['sup_line'], xmin=0, xmax=max(df_user_ts['trial']), linestyles='--', color=color_ms)
plt.hlines(y=df_user_ts['inf_line'], xmin=0, xmax=max(df_user_ts['trial']), linestyles='--', color=color_ms)
plt.hlines(y=df_user_ts['response_ms_med'], xmin=0, xmax=max(df_user_ts['trial']), linestyles=':', color=color_ms)
plt.fill_between(range(len(df_user_ts['trial'])+1), df_user_ts['sup_line'].mean(), df_user_ts['inf_line'].mean(), alpha=0.2)
plt.xticks(df_user_ts['trial'], df_user_ts['symbol'], rotation=90)
grouped = df_symbols.groupby(['userId','timestamp'])['distract_points'].sum().reset_index()
d_point = grouped[(grouped['userId']=='eobt3CosDzEtxWW5P') & (grouped['timestamp']==stamps[0])]['distract_points'].values
plt.title('Event: 1 Score: '+str(max(df_user_ts['correct.answers']))+' Distraction Points: '+str(d_point[0])+' Median Miliseconds: '+str(df_user_ts['response_ms_med'].mean())+' Timestamp: '+str(stamps[0]))
plt.show()

As we might see the points outside of the boundaries are distraction points because they are 2 SD of the median time of response, where the SD corresponds the variance of the group.

The plot below shows the distribution of the time of response in milliseconds on this same event.

In [None]:

plt.figure(figsize=(16, 4))
plt.subplot(1,2,1)
df_user['response_ms'].hist(bins=16)
plt.subplot(1,2,2)
sns.kdeplot(df_user['response_ms'])

Distraction Points Correlated

The first thing to check is the relation that distracting points have with the score performed on every individual, as we know each test has distraction points and scores, we might aggregate per groups, then we can compare if there is any difference between the number of distractions if a person is MS or HC

In [None]:

df_measures_users.groupby('ms').mean()

The table below shows the distractions and scores on each group

Group	Average Score	Average Distractions
MS	52.91	1.81
HC	46.22	1.49

In [None]:

df_ms = df_measures_users[df_measures_users['ms']==1]
df_hc = df_measures_users[df_measures_users['ms']==0]

In [None]:

sns.jointplot("distract_points", "correct.answers", data=df_ms, kind="reg", color=color_ms) #MS correlation
sns.jointplot("distract_points", "correct.answers", data=df_hc, kind="reg", color=color_hc) #HC correlation

As we may see on the plots above we see a negative and significative correlation, the MS group is more clear. The more distractions the less score

The number of distractions that a single person has is a clear feature that helps to classify the MS people, this feature does not deoend in demographic variables but just with in the test behaviour

Plotting All participants, All events

In [None]:

users = list(zip(df_measures_users['userId'], [color_ms if ms==1 else color_hc for ms in df_measures_users['ms']]))
for user in users:
    df_user = df_symbols[df_symbols['userId']==user[0]]
    stamps = df_user['timestamp'].unique()
    if len(stamps) <= 2**2: 
        plot_size =  (2,2); fig_size = (12*1,8*1)
    elif len(stamps) <=3**2: 
        plot_size = (3,3); fig_size = (12*2,8*2)
    elif len(stamps) <=4**2: 
        plot_size = (4,4); fig_size = (12*3,8*3)
    elif len(stamps) <=5**2: 
        plot_size = (5,5); fig_size = (12*4,8*4)
    else: 
        plot_size = (10,10); fig_size = (3*2**10, 2**10)
    plt.figure(figsize=(fig_size[0], fig_size[1]))
    for idx, i in enumerate(range(len(stamps))):
        plt.subplot(plot_size[0],plot_size[1],idx+1)
        df_user_ts = df_user[df_user['timestamp']==stamps[i]]
        plt.scatter(df_user_ts['trial'], df_user_ts['response_ms'], color=user[1])
        plt.hlines(y=df_user_ts['sup_line'], 
                   xmin=0, xmax=max(df_user_ts['trial']), linestyles='--', color=user[1])
        plt.hlines(y=df_user_ts['inf_line'], 
                   xmin=0, xmax=max(df_user_ts['trial']), linestyles='--', color=user[1])
        plt.hlines(y=df_user_ts['response_ms_med'], 
                   xmin=0, xmax=max(df_user_ts['trial']), linestyles=':', color=user[1])
        plt.fill_between(range(len(df_user_ts['trial'])+1), 
                         df_user_ts['sup_line'].mean(), df_user_ts['inf_line'].mean(), color=user[1], alpha=0.2)
        plt.xticks(df_user_ts['trial'], df_user_ts['symbol'], rotation=90)
        plt.ylabel('Response in Miliseconds')
        grouped = df_symbols.groupby(['userId','timestamp'])['distract_points'].sum().reset_index()
        distractions = grouped[(grouped['userId']==user[0]) &
                                    (grouped['timestamp']==stamps[i])]['distract_points'].values
        plt.title('# Test: '+str(idx)+' Score: '+str(
            max(df_user_ts['correct.answers']))+' Distraction Points: '+str(
            distractions[0])+' Median Time: '+str(df_user_ts['response_ms_med'].mean()))

    plt.tight_layout()

Written on August 16, 2018